MPC-Based Optimisation of HIV Drug Treatment

Project Overview

This project develops a Model Predictive Control (MPC) framework to optimise Antiretroviral Therapy (ART) for HIV patients. The primary objective is to regulate viral load and stabilise the immune system while minimising drug intake to alleviate side effects and prevent drug resistance. The system utilises a 5-state nonlinear dynamic model representing the interaction between healthy CD4+ cells, infected cells, viral copies, and the immune response (CTL cells).

Figure 1: The theoretical particle model of HIV used by this repository

Key Technical Features

• Multi-Strategy MPC Design: Implementation of State-Feedback, Output-Feedback (via Luenberger Observer), and Disturbance Rejection MPC.
• Rigorous Stability Analysis: Mathematical proof of asymptotic stability using Lyapunov-based terminal costs and terminal set constraints.
• State Estimation: A Luenberger observer is designed to reconstruct internal states (like infected cell counts) from realistic, measurable outputs like total viral load and CD4+ counts.
• Benchmarking: Performance comparison against a traditional Linear-Quadratic Regulator (LQR) demonstrates MPC's superior stabilisation speed and constraint handling.

Mathematical Framework

The project linearises a complex nonlinear HIV model around a stable equilibrium point representing the symptomatic phase.

• States (x): Healthy CD4+, Infected CD4+, Viral Load (v), CTL precursors, and Killer T-cells (z).
• Control Input (u): Normalised drug dosage (0 to 1).
• Constraints: Enforced positivity on all biological concentrations and physical bounds on medication intake.

File Description

│   README.md
│   LQR.m                               # Benchmark Linear Quadratic Regulator
│   MPC.m                               # Basis MPC implementation
│   MPC_state_feedback.m                # MPC with state feedback, and reference tracking
│   MPC_output_feedback.m               # MPC with observer integration
│   MPC_output_feedback_disturbance.m   # Offset-free MPC for disturbances
│   Stability.m                         # Stability proof of the MPC problem
│   steady_state.m                      # Analysis of the non-linear model (open-loop)

Results Summary

Simulations show that the MPC controller successfully steers the system from a high-viral-load "AIDS state" to a stable "Long-Term Non-Progressor" (LTNP) state.

• Speed: MPC reaches the target viral load faster than LQR.
• Robustness: The output-feedback controller maintains stability even under simulated biological disturbances.

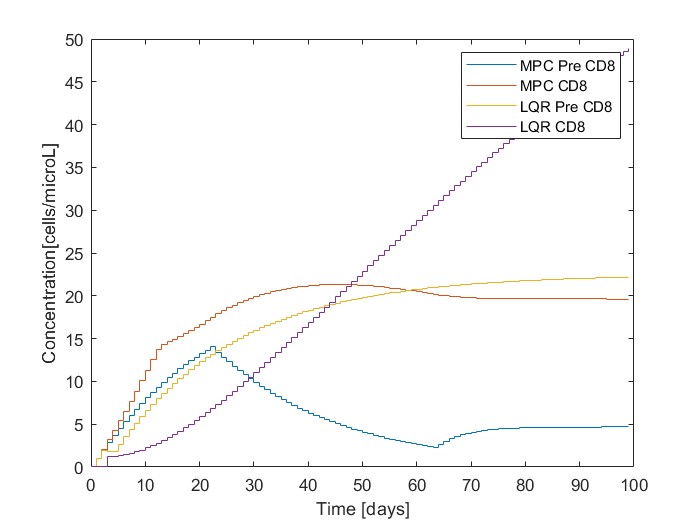
Figure 2: Difference in viral particles between MPC and LQR control strategy

Setup & Usage

• Requirements: MATLAB 2023b or newer.
• Installation: Clone this repository and add the functions folder and all subfolders to your MATLAB path.
• Running Simulations: Execute MPC_state_feedback.m for the primary control demo and Stability.m to visualise the computed region of attraction.

Academic Context

This project was developed as part of the SC42125 Model Predictive Control course at Delft University of Technology (TU Delft).

Authors

Gijs Schlief - MSc Systems & Control / Mechanical Engineering
Jasper Schrauwen - MSc Systems & Control

For technical inquiries, please contact: gijsschlief@gmail.com